What is Standard Deviation? Definition, Formula & Example

Standard deviation is a mathematical concept. 

Often professionals are intimidated by this concept as it involves mathematical calculations; however, you should understand the significance of this important concept. Once you understand the practical application of standard deviation and know the calculations, you will not forget it.

Let us dive in.

Standard Deviation

Definition: Standard deviation is the “Mean of the Mean.” It tells you about the spread of the data. It measured the dispersion of the dataset relative to its mean.

The mean is the average of the given numbers.

If the data points are far from the mean, the deviation is higher within the dataset. This means data spread is more, and so is the high standard deviation. 

Standard Deviation Formula

First, let us analyze a mathematical example of this concept. 

The formula for the population is as follows:

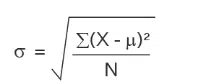
Here,

X = The value of the data distribution

u = population mean

N = Number of observations

The standard deviation formula for sample data is as follows:

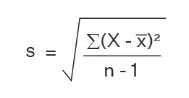
Here,

x bar = sample mean

n = Numbers of observation

Example of Standard Deviation

Your class has five students, and the height of each student is as follows:

First student = 150 cm

Second student = 160 cm

Third student = 170 cm

Fourth student = 165 cm

Fifth student = 155 cm

Calculate the standard deviation.

To calculate the standard deviation, you need the mean and variance. 

Mean = (150 + 160 + 170 + 165 + 155) / 5

= 160 cm

To find the variance, subtract this “mean height” from each student’s height, square it, add them, and take the average.

Variance = [(150 – 160)2 + (160 – 160)2 + (170 – 160)2 + (165 – 160)2 + (155 – 160)2] / 5

= [100 + 0 + 100 + 25 + 25] / 5

= 250 / 5

= 50

Hence, the variance is 50.

Standard Deviation = Square Root of Variance

Standard Deviation = Square Root of 50

= 7.07

Hence, the standard deviation is 7.07 cm.

You might wonder how useful this data is.

These data are essential because they give you the following information:

• The average height of students is 160 cm (mean).
• Most students’ height varies from 152.93 cm (160 – 7.07) to 167.07 cm (160 + 7.07).

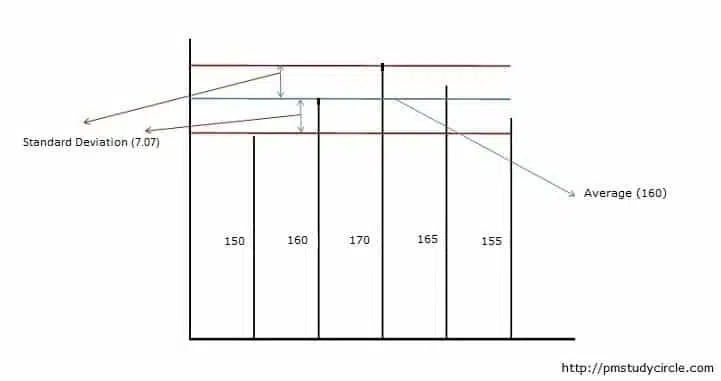
The image above shows the standard deviation for five students. The vertical lines show the height of each student (e.g., 150 cm, 160 cm, etc.). The blue line is the average (or mean) line, and the maroon lines represent the standard deviation.

You can see the drawn standard deviation lines are above and below the average line, and most students’ height lies between these two maroon lines. 

Put simply; you can say that the height of most students is between 152.93 cm to 167.07 cm.

Let us revise the whole procedure once again:

• Calculate the average height of the students
• Subtract the average height from each student’s height and then square it
• Add them together and take the average
• Now take the square root

Important Note

I used population-based data in my example; only five students were in the class.

However, if you select sample data (i.e., choosing a set of random numbers from a large data pool), you will have to divide the variance by (N-1), where N is the number of samples. In other words, if the class has hundreds of students and you select five, divide the variance by (5 – 1) or 4.

You may wonder why we are squaring a number if we take the square root of it.

There is a reason for this calculation; the positive and negative numbers cancel each other out if we add the difference.

Application of Standard Deviation

Standard deviation is useful in analyzing data and is a vital tool for industries, especially clothing manufacturing.

Standard deviation provides information about what size is small, normal, medium, large, or extra-large. Based on the result, the manufacturer sets the size of pants, shirts, and t-shirts.

Standard Deviation Vs Variance

In variance, you take the mean of data, subtract this mean from each data, square the result individually and then take the mean of these squares.

Standard deviation is the square root of the variance.

So, you can say that both provide the same information; however, mathematically, they are different.

The variance shows the data spread size. The bigger the variance, the bigger the spread, so there will be a huge gap between the data. This makes reading the graph difficult. 

Standard deviation is the square root of variance. So even if the variance is bigger, the square root will be smaller, and you can easily see the data dispersion on a graph.

Shown on a graph, the standard deviation is a bell curve around the mean of the dataset. The wider width of the curve shows, the larger the spread of the standard deviation from the mean.

Benefits of Standard Deviation

• Fluctuation in sampling has a minor impact on standard deviation.
• It considers every value in the dataset.
• It is easy to read, understand and communicate.

Limitations of Standard Deviation

• Calculating standard deviation can be complex for a non-technical person
• In standard deviation, extreme values have more weight than the value near the mean
• You cannot calculate the standard deviation in open intervals
• You cannot calculate the standard deviation if the data is in different units

Summary

Standard deviation is a statistical analysis tool that helps industries understand parameters for the entire population by analyzing a sample of data. Although this technique involves mathematical calculation, the concept is straightforward, and standard deviation tells you about the spread of your data. Based on this information, you can develop and market your product.

I hope the standard deviation is clear to you. If you still have doubts, send me a message in the comments section, and I will reply to you. 

Standard deviation is an essential concept from a PMP perspective. You may see a question from this topic on your exam.