Today’s topic of discussion is total float vs free float.
Until I started my PMP exam preparation, I used to think that total float and free float were synonymous.
While reading the Head First PMP book, I came to understand that a network diagram has two different types of floats.
Total floats and free floats are important in developing a network diagram. A better understanding of both will help you draw one and analyze a critical path.
Let’s get started.
Total Float Vs Free Float
Let’s start with total float.
Total Float
Total float is also known as “float.”
Total float is how long an activity can be delayed without putting off the project completion date.
On a critical path, the total float is zero. Total float is often known as the slack.
You can calculate it by subtracting the Early Start date of the activity from its Late Start Date.
Total Float = Late Start date – Early Start date
Or
You can get it by subtracting the activity’s Early Finish date from its Late Finish date.
Total Float = Late Finish date – Early Finish date
Free Float
Free float is how long an activity can be delayed without delaying the Early Start of its successor.
You can calculate the free float by subtracting the Early Finish Date of the activity from the Early Start Date of the next activity.
Free Float = ES of next Activity – EF of Current Activity
Please note that if two activities converge into a single activity, only one of these two activities may have a free float.
A Note on the Convention Used in the Example
You can refer to the first day of your project in two ways. Some experts consider it “one,” while others consider it “zero.”
Both conventions are correct, and you are free to choose. I decided to refer to the first day of the project as “one.”
Here are my reasons:
- The PMBOK Guide follows this convention.
- It seems more logical to me to say, “Hey, today is the first day of the project!” instead of saying, “Hey, today is the zero-day of the project.”
Anyway, you can follow your preference.
The formula used to calculate free float differs for these two situations; however, the result is the same.
I’m assuming that you know how to draw a network diagram, identify the critical path, and calculate the Early Start, Early Finish, Late Start, and Late Finish dates of activities.
If you struggle with these calculations, I have a blog post on the critical path method. Read that post, and then come back.
Examples of Total Float Vs Free Float
Here are two examples of how to calculate free float and total float. The first is easy, and the second one is tougher.
Example: 1
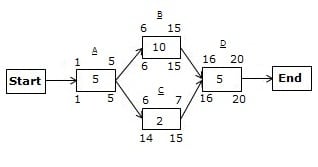
In the above network diagram, you can see two paths:
- The first is A->B->D with a 20-day duration.
- The second is A->C->D with a 12-day duration.
Path A->B->D is the critical path because it has the longest duration.
Calculating the Total Float
Path A->B->D is a critical path; therefore, it will not have a total float.
Path A->C->D is a non-critical path, so it can have a total float.
There are two methods to calculate the total float. For the first, subtract the duration of the non-critical path from the critical path.
For the second method, find the total float for any activity by subtracting the Early Start date from the Late Start date (LS – ES) or subtracting the Early Finish date from the Late Finish date (LF – EF) for any activity.
First Method
Total float = duration of the critical path – duration of the non-critical path
= (duration of the path A->B->D) – (duration of the path A->C->D)
= 20 – 12
= 8
Hence, the total float is eight days.
Second Method
On path A->C->D, Activity A, and D are on the critical path; therefore, they will not have a total float. Only Activity C can.
We can calculate the total float by using either the finish dates or start dates. I will show you both ways.
First, we will go with the Late Finish and Early Finish dates:
Total float for Activity C = (LF of Activity C – EF of Activity C)
= 15 – 7
= 8
Now, the second formula:
Total float for Activity C = (LS of Activity C – ES of Activity C)
= 14 – 6
= 8
The durations are the same, so both formulas will give you the same result.
Calculating the Free Float
From the figure above, you can see that only Activity C can have a free float because all others are on the critical path.
Let’s find it.
Free float of Activity C = ES of next activity – EF of Activity C – 1
= 16 – 7 – 1
= 8
Hence, the free float for Activity C is eight days.
Now we will discuss a more complex example.
Example: 2
Find which activities can have a free float for the below-given network diagram. Calculate it and the total float, considering the duration in days.
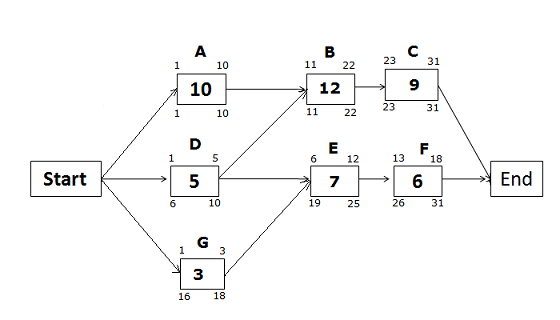
We know that:
Free float = ES of next activity – EF of current activity – 1
In the above diagram, Activity G can have the free float because Activity D and G converge.
Activity D will not have a free float because its successor, Activity E, starts the day after the completion of Activity D.
Free Float for Activity G
We know the formula for free float:
Free float of Activity G = Early Start of Activity E – Early Finish of Activity G – 1
= 6 – 3 – 1
= 2
Total Float for Activity G
Total float for Activity G = Late Finish of Activity G – Early Finish of Activity G
= 18 – 3
= 15
You can see here that the free float for Activity G is two days, and the total float is 15 days.
Summary
Total float and free float are important concepts in schedule management. Total float is commonly referred to as float. Activities on a non-critical path will have a total float. When two activities converge, one of them will have a free float.
Please note that you have to find the total float if you are asked to calculate the float for any activity on the exam.
Here is where this post on total float vs free float ends.
How do you use total float and free float in your project? Please share your thoughts in the comments section.

I am Mohammad Fahad Usmani, B.E. PMP, PMI-RMP. I have been blogging on project management topics since 2011. To date, thousands of professionals have passed the PMP exam using my resources.








Please, why did you subtract 1 from the formula for Free Float?
Hello,
Why for the activity D LF is 10. When we are determining backward pass isn’t it that since E has 2 predecessors D and G, both LF should be 18? I am clear why G has LF = 18, but not why D’s LF = 10? that would be only if we consider activity B as a successor of D, but D has 2 successors, B, and E.
no! reason is because Activity B (which is on the critical path) must start Day 11. So the latest that Activity D (which is a predecessor of Activity B) must finish is Day 10
Only when you decide to do fast tracking you will choose a second longest track not the critical path
Otherwise I will be in critical path only . Then where is the question of float.
Where did A-C-D 12 day duration come from?
5+2+5 = 12
In my opinion, Float, Free Float and Total Float are there for one purpose – to confuse. Take the above example. If activity D is to have zero “free” float then it should be a critical activity, but it is not. In fact activity D can be delayed by as much as 5 days, E by 13 days and F by 13 days, and the project will still complete in 31 days which it has to take in any case if all the activities complete in the estimated duration.
Further, again in my opinion, it is not right when sometimes it is said that the total float is distributed over the path. In the path DEF in the above example, each activity has its own float which it can utilize. The total length of this path is 18 days, which is 13 days short of the critical path. This does not mean that if activity D utilizes its float of 5 days then activities E and F can only be delayed by 13-5=8 days “together”; E and F can be delayed by 13 days each, without going over 31 days critical duration.
In all discussions on this subject, we make the wrong assumption of taking the activities in isolation. We have to remember that all activities are “networked”; hence the term “network” diagram. The best way to establish floats is to do a backward pass. Call the emerging float with any name – free float, total float or simply float – it makes no difference.
Thanks for your feedback Ehsan.
Different formulas and changes to calculate total float to equal to zero, is great to know.
:)
I did not know the difference either or that there even was a difference, good to know…
:)
When total float is zero, will the duration of activities on critical path be zero?
Total float is zero, this means the path is the critical path and all activities on this path will have zero float. Zero float means you can not delay the activity any further. They must finish on the duration assigned to them.
Thanks for the explanations.
You are welcome KPH.
Thank you
You are welcome Abdulrahman.
Thank you so much for this. Has really been helpful.
Although I have question on FF and TT .
From the complex network diagram above, i understand that
path ABC is critical activities= 0 float
path DEF,GEF have floats. Is it OK to say 1) since TT for activity D =5. E= 13. F=13. G= 15. Therefore the total float for the entire project is 15( the highest float number) ?
Or
2) is the floats the highest TF numbr in each path, like Path DEF(5,13,13) = 13
Path GEF (15,13,13) = 15 ?
3) only G has free float ,since it has no successor starting the next day?
Thanka for this article.
You are welcome Ali.
Hello brother is it necessary for Total float and Free float is always will be equal ?
No, they may or may not be equal.
I have this question in my assignment. If activity A has a total float of 10 days and ff of 3 days and if of 7 days. If activity A suddenly delayed by 7 days how many days would activity b get delayed ? How to do it ?
Thank you so much for this! I had a hard time understanding the solving of free float and total float, especially with so many tutorials that uses different formula without a real basis. Anyway, with regards to example number 2, how did you calculate the LS of Activity F? How do you get 26? Thank you!
Hello AC,
Please visit following url to understand these calculations:
https://pmstudycircle.com/2014/01/critical-path-method-cpm-in-project-management/
I’m confused in example 2. while backtracking why did you take 31 at F?? I think so it would b 19 ? as for the activity above to F.
It is 31 because you cannot allow any activity to cross the project completion date.
Free float = ES of next Activity – EF of current Activity -1 (you forgot to mention -1 in your formula)
Where did I forget it?
Just after the second example “Example 2”
“We know that,
Free float = ES of next Activity – EF of current Activity”
Corrected.
Thanks.
Hello Fahad,
Sorry, could you please explain why we need to -1 when calculating free float?
Thanks
If “0” is the project starting day, you will not subtract 1. However, if you start your project from day “1”, you will subtract “1” from the formula.
Hello Becky, I’ll have to see the network diagram to understand the issue.
I have 4 critical paths through my schedule. Three of them I can trace through the project with 1 float on all activities. The fourth path shows critical to an activity and then it literally falls off. How can some of these activities be critical when their successors have float? Does it have anything to do with free versus total?
Well you can not imagine how I am so happy of the blogs. specifically Fahad i so much appreciate your effort to give detailed explanations. God bless u
You are welcome Johnson.
Can I Know what is the independent float
This issue is discussed in above comments.
Can u plz tell me…..calculating free float,float & total float is backward pass or a forward pass?
and one more thing….total float and free float is not calculated for all activities…right???So,how we can know which activity is for calculating free float and total float…….Plzz reply
There are two method of calcuating total float, in one method you need late finish and early finish both, so both passes required. in other method you only need path durations.
In free float, you need early start and early finish. No backward pass is required here.
Please read this blog post to clear your other doubts.
Thanks a lot
You are welcome Tariq.
so fine….i am having exams on network diagrams and u hav explained things to me….Great
I am glad Unice that I could be of some help to you.
Many thanks for this wonderful blog post.
Just one question – how to calculate the Total Float and Free Float from multiple non-critical paths (in your example, we have only one non-critical path, and that’s relatively simple).
for example:
path 1: critical path (float is zero(0)) , activities duration = 33
path 2: non-critical path, activities duration 19
path 3: non-critical path, activities duration 16
path 4: non-critical path, activities duration 14
Path 2 float = 33 – 19 = 14
Path 3 float = 33 – 16 = 17
Path 4 float = 33 – 14 = 19
In this case, what is the project float?
Float is path characteristic, not a project characteristic.
In your case, you will have three floats for three different paths.
I took a course on Project Management in the business school and whenever I use to solve problems on Network diagram – AON was my favorite method to solve scheduling problem – however, as Fahad has already pointed out the non-nomenclatures followed by PMI is start day as 1 and I always choose 0 as my first day however, I got many wrong answers before I familiarize myself with that.
Total slack ( Float ) can’t be there without late pass – if one thinks logically how am I suppose to calculate float for the project without carrying out calculations from both ends – Thus, it is simply subtraction of ES – LS or EF – LF – Yes, they both should have same answers – good way to check.
Ground Rule 2: While drawing ND, when you start plugging values on each node – Left -> Right always choose higher value and add
e.g.,. if the dependency is A->B and there is another dependency C->B if A is ( 0,5 ) if C is (0,7 ) then choose C over A and add the duration to reach B suppose that duration is four which will make it (7,11)
Similarly, backward pass always choose lower value of the two.
Ground rule 3: Free float or Free slack – one has to forget Late values and try to see shortest way to reach other node but there is a twist here suppose if B(3,6) goes to C(8,11) and D(6,15) then free float will be 0 and not 2 – many people make this mistake.
Well said Mr. Nehal.
Hello,
I found your blogs very helpful and useful in clarifying my understanding of this confusing topic. Thanks s o much! I am unfortunately studying to take the exam a 2nd time and I feel as thought I’ve learned a couple of new things here. Hopefully enough to pass!
Good luck on your second attempt Sym.
what is free float of activity D? in example 2
Activity D will not have a free float because its successor activity E is starting on next day of completing of activity D.
This was very helpful. Thanks a lot
I am little bit of Confusion regarding Free Float Formula
1.Free float = ES of next Activity – EF of current Activity – 1
2.Free float = ES of next Activity – EF of current Activity
3.Free float = ES of next Activity – EF of current Activity – Duration of Present
Which Formula is correct from above 1,2,and 3.
Formula 1 & 2 both are correct.
Please read this blog post, this issue is already explained here.
Hi Fahad,
Very good block
Great help for new candidates
Best Regards,
Nutan
Thanks Nutan.
Great Effort Fahad. Although i am not preparing for PMP, but your topic was indeed a great effort in clearing concepts for Management Accounting paper of CA (Pakistan)
Do they have network diagram’s questions in CA exam?
Float or total float can only be calculated for a path and not for an activity. Is this statement true or false?
Plz reply asap. Thank you.
You can calculate the total float for a path and activities on this path can use it.
Who owns the float?
Float is assigned to the path, no body owns it.
Fahad,
You made a mistake on the formula for the Free Float. Right after the definition of the Free Float, you stated that Free Float =ES of the next activity -EF of the current activity.
I think the formula should have been Free Float =ES of the next activity -EF of the current activity -1.
This issue is already explained in the blog post. You will subtract 1 from the formula if the project starting day is “1”.
If the project starts on day “0”, you will not subtract 1 from the formula.
in example 2, you have mentioned Free float of activity G = Early Start of Activity E – Early Finish of Activity G – 1
whats this -1 means,pls help
Since I have assumed the first day of starting the project is “1”, I will have subtract it from the formula. If you start from zero, you don’t have to do it.
Send me more diagrams of network analysis with calculated total and free floats. Am in Kenya and my email address is [email protected]
You can draw the diagram on your own, and try to solve it.
In the diagram used for example 2, how total float do we have?
31-18=13 and
31- 16= 15
Doest it mean if asked to calculate the float (free float) in diagram 2 it would have 2 answers ie 13 and 15 as the float?
Pls explain.
Thanks
Every path will have its own float.
Hello Fahad.
First, thank you for the lesson!
Please advise my understanding.
On D-B-C path, am i correct to say the Activity “D” has a free float of 5 days to its successor Activity “B”.
* I am still struggling to fully understand the influence of Free Float in Total Float
Thank you
Activity E is starting just after completing the activity D, so activity D can not have a free float.
Hi,in th
So in your example 2 the total float for the project is 33 (5+13+15), is that correct? What is the secret for calculating total float for the project? It is just adding all floats for all of the activities in the project together isn’t it?
Please read this blog post on critical path method:
https://pmstudycircle.com/2014/01/critical-path-method-cpm-in-project-management/
Is Free Float same as Buffer ?
No, they are different.
Please read below given blog post to understand the buffer:
https://pmstudycircle.com/2014/02/critical-chain-method-ccm-in-project-management/
thank you very much. your explanation has made a lot of difference. Please let me know if my understanding is correct: 1. Free float can be calculated only for activities that share a common successor (in this case F and C have a common successor in “end”) and 2. the formula would be “ES of the next activity – Early Finish Date of the current activity” (no subtracting 1 even if we start with 1 as the start date). It would be great if you could come. Thanks for sharing knowledge.
As per my understanding you will have to subtract 1 in this case as well.
Is this an AON diagram? Some nodes are hard to read. Total float can be vary here.
Regards,
Creately
Which diagram are you talking about?
What is the significance of free float?
It gives extra margin to an activity.
Fahad sb Jazak Allah for replying and clarifying. I have another question regarding total float and free float, which is,
What does mean by total float is owned by owner and free float is owned by contractor?
I saw this in above comments.
Total float may affect the project completion date which is a concern of client.
Regarding the free float, it just affects the early start of next activity and client does not care about it. It is up to you to manage it. Client rarely interfere that how you manage the individual activities.
Jazak Allah, Now its clear.
I am confused how FF differs from Total Float. If Total Float is shared for the projects at 15, and activity G has FF of 2, where and which activity can be delayed by 15 days without affecting the project completion date? I see perfectly how FF works but not how Total Float could be used/applied.
Total float is for a path. If any activity delays, it will eat total float.
I’m very lucky to get the explanations and examples so easily explained by you…..really appreciated and thanks a lot for writing such a wonderful blog….thanks again…
You are welcome Vijay.
Your explanation on every topic is wonderful. I will practice the calculation with the similar example you used for your calculation and then I think I’ll be able to perform all the calucations with difderent examples.
I’m glad it helped you understand the concept.
Dear Fahad,
I beg to differ on your explanation on FF. As per the definition of FF, “it is the duration by which an activity can be delayed without impacting the ES of the successor activity or successor activities.
Therefore for activity D the FF is ZERO, as any delay in activity D will impact the ES of Activity E, eventhough it doesnot impact activity B. Similarly the FF of activity G is ZERO, as any delay in activity G will impact the ES of Activity H, eventhough it doesnot impact activity E.
As I understand FF of an activity is NOT calculated by taking the largest ES date of its successors, and it is just governed by the above DEFINITION.
Most importantly, the activities having FF in the network are:
Activity F= 31-18= 13 days
Activity I=31-13= 18 days
Loading the above network to a CPM software could thoroughly validate my explanation.
Total Float and Free Float are different.
An activity will have a free float only when it has two successors activities.
Hope it helps.
I am sorry to say your explanation on FF is flawed. It is NOT true that an activity will have a FF only when it has 2 successor activities.
Infact FF can only occur when 2 or more activities share a common successor and not the other way. As I said before the only activities having FF in the network are activities F and I.
I am only replying for the benefit of others, as I have seen in this string many people (Khaled, Joe, HB, Sadek etc) raising the same question to you on FF.
I meant that, to have a free float an activity should have more than one successor activity. It can have two successor activities or three…
For more clarification, you can visit the pmbok guide, page 177, which says..
free float is the amount of time that a schedule activity can be delayed without delaying the early start date of any successor or violating a schedule constraints.
Hello Murali,
Let me explain you in this way.
The PMBOK Guide says that
“free float is the amount of time that a schedule activity can be delayed without delaying the early start date of any successor or violating a schedule constraints.”
And you says that Activities F and I will have a free float. How they can have it because they are last activities on their respective path, and therefore they are not affecting the early start of their successor activities.
Now you are saying that activity D is not having the free float.
Let us see if the PMBOK Guide’s definition is applying here.
Activity D is finishing on 5 day.
Its successor Activity is B, which is starting on 11 day.
Now you can clearly see that activity D can be delayed for 5 days without affecting the early start of Activity B. This is exactly the PMBOK Guide is saying. Please read the definition again.
Hence the Activity D will have free float of 5 days.
Is it clear?
If there was an activity before END, then the F and I would have a free float that would be the same as total float as you explained in the first simple example.
On the other hand, if you had an activity right after START branching out to A, D and G, then the activity would not have a free float despite the fact that it had multiple successors.
If you delete H and I from the diagram, G would have free float of 2 days and total float of 15 days even though it does not have multiple successors. It shares E as successor with D.
In your diagram, D and G would violate E and H respectively if they are delayed though it would not affect critical path right away.
I am not sure if D and G really have a free float when they violate one of the successors as long as it does not affect critical path.
I would appreciate if you check again and clarify.
Hello Bryan,
You are right, free float will occur when two or more activities shares a common successor.
I have amended this blog post as well.
Dear Fahad,
Let me explain my position as below:
“free float is the amount of time that a schedule activity can be delayed without delaying the early start date of “ANY” successor or violating a schedule constraints.”
Please note the word ‘ANY’ from the above definition:
For activity D, it has 2 successors namely activity B and activity E. All the while in your explanation you are talking about FF of activity D with respect to Activity B (first successor) only, what about its impact on activity E (the second successor)????
Can we delay the activity D without delaying the ES of Activity E?, and the answer is NO. Therefore as per definition the activity D has Zero FF.
The same logic goes to activity G, which also has ZERO FF, as it is delaying the ES of activity H.
Nowhere in the defintion it talks about taking the greatest ES amongst its successors while calculating the FF of an activity.
Nowhere in the defintion it talks about taking only ONE successor while calculating the FF of an activity.
Also it is NOT MANDATORY to have multiple successors to have a FF, even activities with a single successor can have FF provided you have a CONVERGING network.
That is the reason why FF is more stringent than a TF. The reason being, for a FF all the activities are to be completed as per their ES dates.
Therefore in a project, the TF is owned by the Owner/client and the FF is owned by the Contractor.
Now coming to activities F & I, both of them have a successor activity END (which is a milestone activity with duration ZERO). As the CP duration is determined as 31 days, the activity F has a FF of 31-18= 13 days and activity I has a FF of 31-13=18 days. Coincidentally they are equal to their respective Total Floats as well.
As I mentioned in my first reply, please update this logic in a CPM software like P3, P6 or MS Project and they will validate my explanation.
Please send me your network diagram at [email protected]
You are right that when two or more activity will converge, they may have free float. I have corrected this error in my blog post.
Regarding your second point:
You are saying that Free Float of F = 31 – 18,
This means Free Float of F = Late Finish of F – Early Finish of F
Are you sure?
I believe you are calculating total float and mixing it with free float.
Formula to calculate free float is
Free Float of an activity = ES of next Activity – EF of Activity
As the activity END is a milestone activity (Zero duration), its ES is 31 and EF is 31.
FF of activity F= ES of activity END – EF of Activity F
=31- 18= 13 (In other words activity F can be delayed by 13 days without delaying the ES of activity END or project completion)
FF of activity I= ES of activity END – EF of Activity I
=31- 13= 18
Now coming to Total Floats,
TF of activity F= LF of activity F – EF of activity F
= 31 – 18 = 13 days
TF of activity I= LF of activity I – EF of activity I
= 31 – 13 = 18 days
Therefor for activities F & I, the TF and FF are the same.
Hope this clarifies.
Okay.
Yes, you’re right Murali that free float will occur when two activities share a common successor.
Thanks for pointing out this mistake in this blog post and I thank you for the same.
Dear Fahad,
You are welcome.
I am happy that I could contribute to your popular website for prospective PMPs.
Please continue your good work for the PM community.
Dear Mr Fahad
Thanks for nice explanation,
Can you explain the examples of network diagrams with leads and lags e.g Finish to Finish, Start to finish, Start to Start.
Hello Ahmad,
The example given in this blog post is enough for the PMP exam. Anyway, I have noted your request and once I get some time, I will update this post with more examples as you requested.
Thanks Fahad
I will be wait for your comment.
I appreciate your lucid explanation on the topic.
Thanks Fahmi.
free float = minimum early start of succesor – Late finish
NOT THE GREATER EARLY START
What did you mean?
Hi
I think if there is more than one successor activity,we must take the least in early start not the greater … I want explain this point why u take the greater….it seems not logical to me
I think you are talking about the forward pass, when an activity has two predecessor activities, and we take the greater early finish date to calculate the early start of successor activity.
Okay.
Let us say activity C has two predecessor activities, activity A and activity B. It means activity C can not be started until its predecessors activities complete. If activity A finishes in 5 days and Activity B finishes in 10 days, activity C will only start after 10 days, because until both activities complete, activity C can not be started.
Hope it helps.
Hello Fahad
Seriously this blog and notes has prevented me from tearing my hair :). I initially just knew the definition of free float but never had to calculate it on any of the questions I came across, I came across it on the first pmp exam which I took and failed. Finally found a free float calculation question on oliver lehmann today and was confused by the answer. I found more confusing answers on pmzilla, different people had different opinions on how to calculate it. I was really frustrated seeing so many answers and not knowing for sure how to calculate it. even the first website that came up on google when I typed “how to calculate free float” explained it, but I was still not confident in trusting it. However your blog explains it completely with an example. I am confident now. Thanks a lot man..really really appreciate it. I will keep looking for more questions that I have on your blog. This is my second time preparation for the pmp. I have gone through 5 books in total: Rita, achieve pmp success, kim heldman and pmp head first. The last 2 I have just gone through the questions, since I felt the explanation is the same across the books. I am in the process of completing as many sample exams I can come across, I have been doing okay averaging 70% across all, some tough some easy. Sorry….digressed from my initial comment..thanks a lot once again.
– Daniel
Hello Daniel,
I am sorry to hear that you have failed the exam in your first attempt. I hope you will pass the exam in your next attempt. Just work on improving your weak spot.
Don’t go for many books. Two books with the PMBOK Guide is more than enough to pass the exam.
Fahad
I’m attempting to calculate the date by which a task must be completed so it won’t delay the subsequent task(s), in Project 2007. I’m using Free Float added to the Finish date. Most of the returned dates make sense. However, a few don’t. I haven’t identified a pattern to the exceptions yet. Any thoughts on this?
Sorry Mike, I don’t have a good idea about MS Project.
Thanks for your detailed explanation on Total Float vs Free Float. Sir, i’ve not gotting the concept of RACI Chart and thus cannot answer PMP questions on it, pls i need you assistance.
Thanks for your detailed explanation on Total Float vs Free Float. Sir, i’ve not got the concept of RACI Chart and thus cannot answer PMP questions on it, pls i need you assistance.
RACI stands for responsible, accountable, consulted, and informed. It is a responsibility assignment matrix where you list the name of person and mention that whether he is responsible, accountable, consultant, or informed for a particular process.
one other type of float in independent float :”is the maximum amount of time an activity can be delayed without delaying the early start of the succeeding activity and without being affected by the allowable delay of the preceding activities”.
The PMBOK Guide recognizes only two types of float; i.e. total float and free float.
Also There is one other type of float in which is interferring float ” is the maximum amount of time an activity can be delayed without delaying the entire project but delay the early start of the succeceding activities.
Well, Interfering float = Total float – Free Float, i.e. amount of total float which is not available.
Do you have anything describing total float vs. free float when you have start-to-start, finish-to-finish, and start-to-finish links along with leads and lags?
I took the simplest example to explain the concept. As of now I don’t have any start-to-start, finish-to-finish, finish-to-start and start-to-finish relationship diagram with leads and lags explaining the float concept.
But in future I might write on it.
hi,
can you please explain how do we calculate a float for a particular node, like what is the float at node B?
In the given example we have two paths; i.e. ABD and ACD. The duration of the path ABD is 20 days, and the duration of path ACD is 12 days.
Obviously, the path ABD is the critical path, and float on critical path is always zero. Therefore the float for activity B is zero.
However, you can calculate the float for the path ACD, which is (20 – 12); i.e. 8 days. Therefore flat for activity C will be 8 days.
thanks a lot Fahad for the explanation
If there was a diagrammatic solution it would be easy to understand more. I suggest draw stuff from a diagram solution like http://creately.com
Thanks Shalin for sharing the link.
Hi Fahad, Thanks for the explanation and a good diagram, now i can calculate them. Looking ahead for the next post in CPM for more complex diagrams and their calculations. thankyou
Soon you will see them.
Update:
Hello Drew,
here is the post on critical path method with more complex diagram and calculation.
https://pmstudycircle.com/2014/01/critical-path-method-cpm-in-project-management/
I am unable to see the network diagrams on any of the questions of explanations like the one above for total and free float.
Thanks for your compliments Ayushman!
Can you please give me an example where total float of an activity is not same as free float of that same activity.
Hello Kishore,
In fact, I was also planning to draw a network diagram where you can see that the total float and free float are different but in that case, calculation will little lengthy. So I avoided it.
I covered concept to calculate the total float and free float in this example and I hope once you understand it, you can calculate them in any scenario.
Even if you’re having any problem with it, send me scanned copy of diagram, I will try to explain it to you, or wait for my other blog post in CPM where I will calculate the total float and free float for more complex diagrams.
Hi friend
For activity G, if the total float is 15 days, how comes that the successor activity E starts at day 6?
I think that I am confused about the real meaning of total float!
Total float is an amount of delay that an activity can be delayed without affecting the project end date. Please note that, for a critical path, total float will be zero.