Critical Path Method (CPM) in Project Management

This is the most comprehensive post on the Critical Path Method (CPM). In this post, I will explain the CPM, the step-by-step process for developing a CPM network diagram, an example of it, and its pros and cons.

The Critical Path Method is the oldest and most popular method for developing network diagrams and project schedules. It shows the critical path, which is the path with the longest duration that must be completed to complete the project.

The Critical Path Method is often known as “Critical Path Analysis (CPA)” because it shows a critical path, critical activities, logical relations between activities, and their independence from each other.

Background of Critical Path Method

CPM was developed in the 1950s by the U.S. Navy and DuPont Corporation. It was originally used for large-scale construction projects. Today, CPM is used in many industries, including engineering, manufacturing, and software development.

CPM works by creating a network diagram that shows the sequence of tasks in a project. Each task is assigned a duration and dependencies on other tasks. The critical path is the longest path through the network diagram, determining the project’s completion time. If any task on the critical path is delayed, the entire project will be delayed.

What is the Critical Path Method (CPM)?

The Critical Path Method is a project management technique for planning, scheduling, and controlling project tasks. It identifies the longest sequence of dependent tasks (known as the “critical path”), which must be completed on time to ensure that the project meets its deadline. The critical path’s duration determines the shortest possible project completion time. Tasks on this path are crucial because delays in any of these tasks will also delay the entire project. 

CPM helps managers allocate resources efficiently, identify potential bottlenecks, and optimize workflows to ensure timely project delivery.

You can define a critical path as:

• the longest path in the network diagram or
• the shortest duration required to complete the project.

The above statements may appear to be opposites, but they convey the same message.

For example, let’s say you have a project to construct three buildings. The first is the largest, the second is medium-sized, and the third is the smallest. You will develop the network diagram comprising three paths, each representing a building.

You will then calculate the duration for each path. The first building lasts 31 months; the second will take 18 months, and the third will require 13 months.

The first path is for the largest building, the second is for the medium-sized one, and the third is for the smallest building.

Now, let us review the diagram for Critical Path Analysis.

Did you notice that the first path is the longest? 

It is 13 months longer than the second and 18 months longer than the third. This means that you can wait 13 months and then start working on the second building because you can complete the second building in 18 months.

Likewise, you could wait 18 months and start working on the third building because it will take 13 months to complete. This means that even if you start work on the third building 18 months after the project’s start date, you can still finish it on time.

This waiting period is known as float or slack.

So, which is the critical path in this network diagram?

It is the longest path on the network diagram because you cannot complete your project before finishing the first building. Although you can complete the other two buildings quickly, your project is not considered complete until the first building is completed.

This confirms the first statement, “The critical path is the longest path on the network diagram.”

Now, what is the shortest duration required to complete the project?

It is 31 months because you cannot complete your project in less time, which is the critical path’s duration.

This supports the second statement, “The critical path is the shortest duration in which you can complete the project.”

So, both definitions are the same.

In ideal conditions, a network diagram should have one critical path. Multiple critical paths can create difficulties. 

The critical path has the longest duration and is the total project duration. Activities on the critical path have no float; therefore, you must ensure they are completed on time. Any delay in a critical activity (critical path activity) will delay the project.

Critical Path Method Definition

Here are a few definitions of the Critical Path Method by recognized authorities and organizations:

1. Project Management Institute (PMI)

PMI defines CPM as “a method used to estimate the minimum project duration and determine the amount of scheduling flexibility on the logical network paths within the schedule model.”  

Source: A Guide to the Project Management Body of Knowledge (PMBOK Guide), 6th Edition

2. Association for Project Management (APM)

APM describes the Critical Path Method as “a scheduling technique used to identify the sequence of activities that must be completed on time for the entire project to be completed on schedule. It identifies tasks that are critical and those that have float.”  

Source: APM Body of Knowledge, 7th Edition

3. U.S. Government Accountability Office (GAO)

GAO defines CPM as “a schedule analysis technique used to identify the sequence of tasks that determines the overall project duration. Delays in any task on the critical path directly impact the project’s end date.”  

Source: GAO Schedule Assessment Guide, Best Practices for Project Schedules

Float or Slack in CPM Diagram

In the Critical Path Method, float or slack is the time in which a task can be delayed without affecting the project’s deadline or the start of the next task. It can help you see flexibility in task durations.

There are two main types of float:

1. Total Float: This is how long a task can be delayed without affecting the project’s end date. For example, a task with a total float of three days can be delayed by three days without changing the project’s completion date.

2. Free Float: This is the duration in which a task can be delayed without affecting the start date of the next task. It is specific to the task, as well as its immediate successor in the project schedule.

Tasks on the critical path have zero float because any delay in these tasks will directly delay the whole project. Tasks not on the critical path may have float, allowing more flexibility. 

Understanding float helps you prioritize tasks. You can focus on tasks with no or little float to prevent project delays and use tasks with float for flexibility if resources are tight.

Contingencies and Constraints in CPM Network Diagram

Fast-tracking and crashing are two ways to compress the schedule when it is behind the planned progress or needs to finish earlier. They both help reduce the project duration differently.

Fast Tracking

Fast-tracking means doing some tasks simultaneously instead of one after the other. Normally, tasks are done in sequence, meaning one task has to finish before the next can start. But with fast tracking, you overlap the tasks. 

For example, if Task A has to finish before Task B can start, you begin Task B before Task A is completely done. This saves time but adds risk because overlapping tasks can cause mistakes or rework if one task depends too much on the other. 

Fast-tracking is useful when you want to save time without spending extra money. However, it works best when tasks can overlap without too many problems. You must manage and monitor fast-tracked tasks carefully to avoid errors, which will increase risks.

Crashing

Crashing means adding more resources (e.g., money, equipment, or people) to speed up tasks on the critical path. For example, if a task takes 10 days with two workers, then you might reduce the time to five days by adding two more workers. Crashing costs more because you must pay for extra resources, but it can be helpful when time is more important than budget.

Crashing works well when adding resources, which can speed up a task. But sometimes, more people or equipment don’t help, leading to inefficiency. Crashing increases costs, so it should only be used when necessary.

Step-by-Step Process for Using the Critical Path Method

To use the Critical Path Method, you must break the project into a work breakdown structure until you reach the work-package level. Afterward, you will break the work package into activities to develop the CPM network diagram.

The steps to develop a network diagram using the Critical Path Method are as follows.

Step 1. Identify Activities

Start by listing all the tasks required to complete the project. Break down the project into smaller, easy-to-manage work packages and then activities. Each task should be clear, specific, and have a defined start and end.

Example: Building a house involves laying the foundation, building walls, and installing the roof.

Step 2. Sequence Activities

Once you have a list of activities, arrange them in the order that they must happen. Some tasks must be completed before others can start, while some can happen simultaneously. You must figure out the correct order for all tasks. 

Example: You can’t install the roof before building the walls.

Step 3. Find Dependencies and Relationships

After sequencing the activities, identify the dependencies and logical relation between tasks. Relationships show how one task relies on another to start or finish. 

There are four types of relationships:

1. Finish-to-Start: Task A must finish before Task B can start.
2. Finish-to-Finish: Task A must finish before Task B can finish.
3. Start-to-Start: Task A must start before Task B can start.
4. Start-to-Finish: Task A must start before Task B can finish.

Example: Laying a foundation must be finished before you can build walls.

Step 4. Estimate Activity Resources and Durations

Now, estimate how long each task will take and what resources (like workers, materials, or equipment) you will need. This will help you determine the time and effort required for each activity. 

Example: Building walls may take five days with three workers.

Step 5. Create a Network Diagram

Next, draw a network diagram representing the sequence of activities and their dependencies. Use boxes to show each task and arrows to indicate their order and connections. This diagram will help you see how tasks are connected and what needs to be done first.

Example: Draw boxes for tasks like “Laying Foundation” and “Building Walls,” and connect them with arrows showing the order.

Step 6. Find the Critical Path

Now, determine the longest sequence of tasks that controls the shortest time required to complete the project. This is called the “critical path.” To find it, add up the duration of each path in your diagram. The longest path is critical because it shows the tasks that cannot be delayed without delaying the entire project.

Example: If “Laying Foundation,” “Building Walls,” and “Installing Roof” is the longest path, that is the critical path.

Step 7. Optimize the Schedule

Finally, optimize your schedule by balancing resource use. Resource leveling adjusts the schedule to ensure no resource is overworked, while resource smoothing adjusts the schedule to make better use of resources without overloading them. This helps avoid bottlenecks and ensures smooth progress throughout the project.

Example: If too many tasks need the same workers simultaneously, delay non-critical tasks to free up workers.

This process will help you create and manage the project schedule more efficiently.

Commonly Used Terms in the Critical Path Method

Before we discuss how to find the critical path, let us understand a few commonly used terms in a critical path network diagram:

• Critical Path: This is the longest sequence of dependent tasks, which determines the shortest project completion time.
• Activity: This is a specific task in a project with a defined start and end.
• Duration: This is the total time required to complete an activity.
• Early Start (ES): This is the earliest time that an activity can start without delay.
• Early Finish (EF): This is the earliest time that an activity can finish.
• Late Start (LS): This is the latest time that an activity can start without delaying the project.
• Late Finish (LF): This is the latest time that an activity can finish without causing a delay.
• Float (Slack): This is the time that a task can be delayed without affecting the project’s overall timeline.
• Predecessor: This is a task that must be completed before another can start.
• Successor: This is a task that follows another in sequence.
• Milestone: This is a significant point or event in the project timeline that marks the completion of a major phase.
• Dependency: This is the relationship between tasks, in which one task’s start or end is dependent on another’s completion.

Critical Path Method Example

Based on the network diagram below, identify the total paths, critical paths, and float for each path.

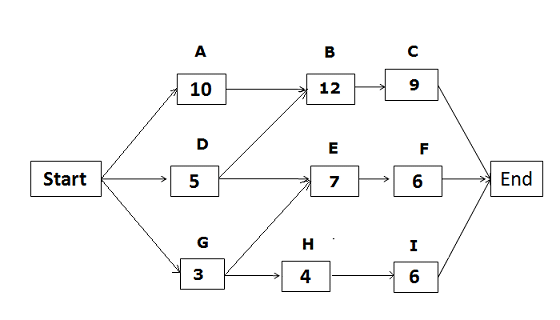
The above network diagram has five paths.

The paths and their durations are:

1. Start -> A -> B -> C-> End (Duration: 31 days)
2. Start ->D -> E ->F -> End (Duration: 18 days)
3. Start -> D -> B -> C -> End (Duration: 26 days)
4. Start -> G ->H ->I -> End (Duration: 13 days)
5. Start -> G -> E ->F -> End (Duration: 16 days)

The first path is the critical path since its duration is the longest. The float on the critical path is zero.

The float for the second path “Start ->D -> E ->F -> End” = duration of the critical path – duration of the path “Start ->D -> E ->F -> End.”

= 31 – 18 = 13

Hence, the float for the second path is 13 days.

Using the same process, we can calculate the float for other paths.

Float for the third path = 31 – 26 = 5 days.

Float for the fourth path = 31 – 13 = 18 days.

Float for the fifth path = 31 – 16 = 15 days.

Calculate Early Start, Early Finish, Late Start, and Late Finish

We have identified the critical path and the duration of the other paths. Now, it’s time to move on to more advanced calculations: Early Start, Early Finish, Late Start, and Late Finish.

Calculating Early Start (ES) and Early Finish (EF)

To calculate the Early Start and Early Finish dates, we use the forward pass; we will start from the beginning and proceed to the end.

The Early Start (ES) for the first activity on any path will be 1 because you cannot start the activity before the first day of your project.

The starting point for any activity is the endpoint of the predecessor activity on the same path (plus one).

The formula used for calculating Early Start and Early Finish dates is:

• Early Start of the Activity = Early Finish of Predecessor Activity + 1
• Early Finish of the Activity = Activity Duration + Early Start of Activity – 1

Early Start and Early Finish Dates for the Path Start -> A -> B -> C -> End

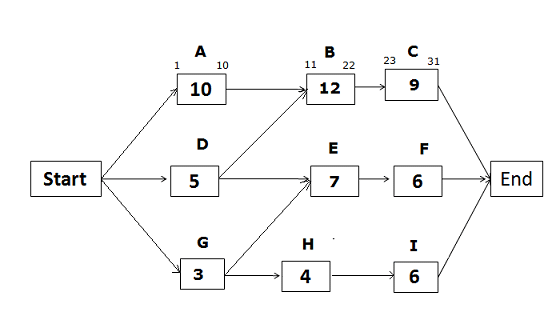
Early Start of Activity A = 1 (since this is the first activity of the path)

Early Finish of Activity A = ES of Activity A + Activity Duration – 1 = 1 + 10 – 1 = 10

Early Start of Activity B = EF of Predecessor Activity + 1 = 10 +1 = 11

Early Finish of Activity B = ES of Activity B + Activity Duration – 1 = 11 + 12 – 1 = 22

Early Start of Activity C = EF of Predecessor Activity + 1 = 22 +1 = 23

Early Finish of Activity C = ES of Activity C + Activity Duration – 1 = 23 + 9 – 1 = 31

Early Start and Early Finish Dates for the Path Start -> D -> E -> F -> End

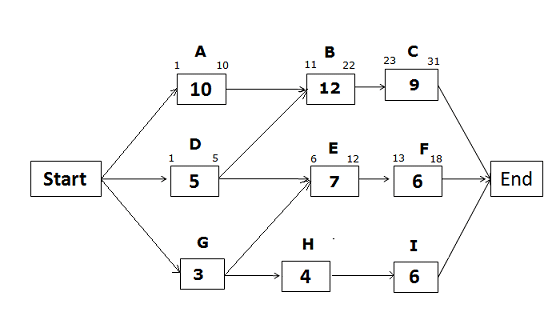
Early Start of Activity D = 1 (since this is the first activity of the path)

Early Finish of Activity D = 1 + 5 – 1 = 5

Early Start of Activity E = EF of Predecessor Activity + 1

Since activity E has two predecessor activities, which one will you select? The answer is the activity with the greater Early Finish date. The Early Finish of Activity D is 5, and the Early Finish of Activity G is 3 (we will calculate it later).

Therefore, we will select the Early Finish of Activity D to find the Early Start of Activity E.

Early Start of activity E = EF of Predecessor Activity + 1 = 5 + 1 = 6

Early Finish of Activity E = 6 + 7 – 1 = 12

Early Start of Activity F = 12 + 1 = 13

Early Finish of Activity F = 13 + 6 -1 = 18

Early Start and Early Finish Dates for the Path Start -> G -> H -> I -> End

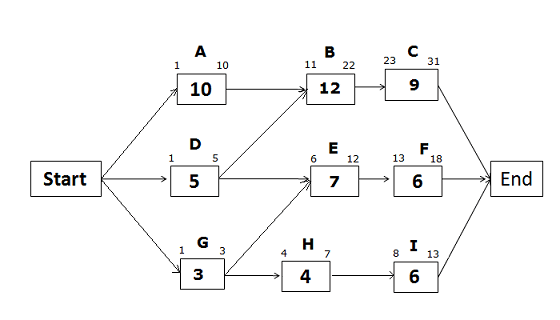
Early Start of Activity G = 1 (since this is the first activity of the path)

Early Finish of Activity G = 1 + 3 – 1 = 3

Early Start of Activity H = 3 + 1 = 4

Early Finish of Activity H = 4 + 4 – 1 = 7

Early Start of Activity I = 7 +1 = 8

Early Finish of Activity I = 8 + 6 – 1 = 13

Calculating Late Start (LS) and Late Finish (LF)

We have calculated the Early Start and Early Finish dates of all activities. Now it is time to calculate the Late Start and Late Finish dates.

The Late Finish date of the last activity on all paths will be the same because no activities can continue once the project is completed.

The formula used for Late Start and Late Finish dates is:

• Late Start of Activity = Late Finish of Activity – Activity Duration + 1
• Late Finish of Activity = Late Start of Successor Activity – 1

To calculate the Late Start and Late Finish, we use the backward pass; i.e., we will start from the last activity and move back towards the first activity.

Late Start and Late Finish Dates for the Path Start -> A -> B -> C -> End

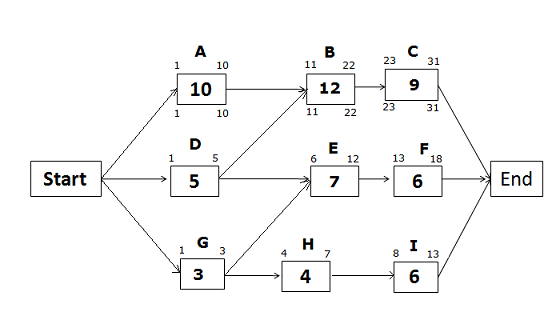
On a critical path, the Late Start and Late Finish dates will be the same as the Early Start and Early Finish dates.

Late Start and Late Finish Dates for the Path Start -> D -> E -> F -> End

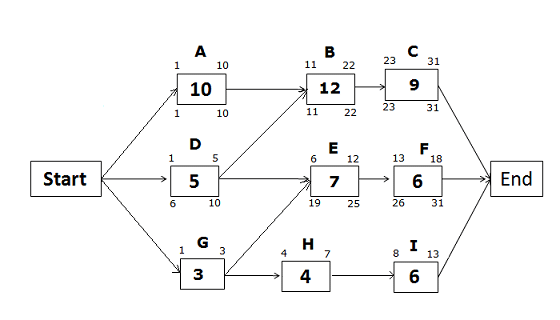
Late Finish of Activity F = 31 (because you cannot allow any activity to surpass the project’s completion date)

Late Start of Activity F = LF of Activity F – Activity Duration + 1 = 31 – 6 +1 = 26

Late Finish of Activity E = LS of Successor Activity – 1 = LS of Activity F – 1 = 26 – 1 = 25

Late Start of Activity E = LF of Activity E – Activity Duration + 1 = 25 – 7 + 1 = 19

Late Finish of Activity D = LS of Successor Activity – 1

If you look at the network diagram, you will notice that activity D has two successor activities, B and E. So, which activity would you select?

You will select the activity with the earlier (least) Late Start date. Here, the Late Start of activity B is 11, and the Late Start of activity E is 19.

Therefore, you will select activity B, which has the earlier Late Start date.

Hence,

Late Finish of Activity D = LS of Activity B – 1 = 11 – 1 = 10

Late Start of Activity D = LF of Activity D – Activity Duration + 1 = 10 – 5 + 1 = 6

Late Start and Late Finish Dates for the Path Start -> G -> H -> I -> End

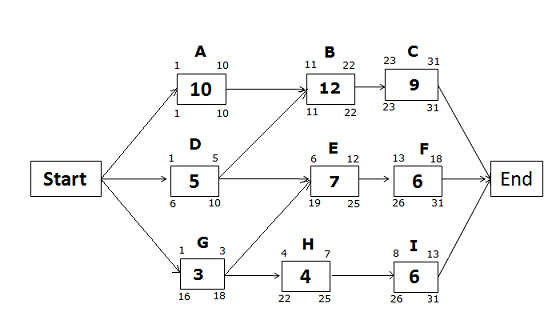
Late Finish of Activity I = 31 (because you cannot allow any activity to surpass the project’s completion date)

Late Start of Activity I = 31 – 6 + 1 = 26

Late Finish of Activity H = 26 – 1 = 25

Late Start of Activity H = 25 – 4 + 1 = 22

Late Finish of Activity G = 19 – 1 = 18 (we will choose the late start of Activity E, not Activity H because the Late Start of Activity E is earlier than the Late Start of Activity H)

Late Start of activity G = 18 – 3 + 1 = 16

Calculate the Free Float

Before proceeding further, I recommend reading my blog post on “Total and Free Float” to better understand them.

Visit: Total Float and Free Float

The formula for the Free Float is: Free Float = ES of Next Activity – EF of Current Activity – 1

Critical Path Method Vs PERT

PERT focuses on duration and is used when the project has uncertain activity durations. It is more useful in projects where the time to complete each task is unknown. You use three estimates in PERT: optimistic, pessimistic, and most likely. This helps you calculate the average duration for each task. PERT is mostly used in research, development, and other projects with uncertainties.

CPM focuses on both time and cost. It is used when task durations are more predictable and you want to manage both the schedule and the budget. CPM assumes you know the exact duration for each task, and it helps you find the longest path (critical path) to finish the project on time. CPM is more common in construction and manufacturing projects with well-defined timelines and cost estimates.

Critical Path Method Vs Critical Chain Method

The main goal of CPM is to ensure that tasks on the critical path are completed on time. It assumes resources (like people and equipment) are always available when needed.

Critical chain project management focuses on managing both tasks and resources. It recognizes that resources are often limited and may not always be available when needed. CCPM builds a “buffer” or extra time into the schedule to protect the project from delays caused by resource constraints or unexpected issues. This buffer helps the project stay on track despite small delays.

CPM focuses on managing tasks and assumes resources are available, while CCPM focuses on managing tasks and resources, with extra time built into the schedule to handle delays. CCPM is often better for projects with limited resources and a lot of uncertainty

Critical Path Method Vs Gantt Chart

A Gantt chart is a visual timeline that shows tasks and when they will happen. It displays tasks as horizontal bars, with the length of each bar representing the duration of each task. You can easily see when tasks start and end, how long they will last, and which tasks overlap or happen simultaneously. It is a simple, great way to track progress and see the project schedule visually.

CPM helps you understand which tasks are crucial and where delays can cause problems. It is more detailed in calculating task durations and dependencies but less visual than a Gantt chart.

A Gantt chart provides a clear visual timeline of tasks, while CPM focuses on identifying the critical tasks that control the project’s schedule.

Why Must You Monitor Non-Critical Paths in a Network Diagram?

You must monitor the non-critical path in a network diagram because delays in non-critical tasks can impact the project if not managed properly. While the critical path shows the tasks directly affecting the project’s completion time, the non-critical tasks also keep the project running smoothly.

Here are some key reasons to monitor non-critical paths:

• Slack Utilization: Non-critical tasks have “slack” or “float,” which means they can be delayed without immediately affecting the project deadline. However, if these delays pile up or use all the slack, they can affect the critical path and delay the project.

• Resource Availability: Non-critical tasks still use resources (e.g., workers, materials, or equipment). If these tasks aren’t managed well, resource shortages can arise, thus causing delays for critical tasks.

• Criticality: Sometimes, project changes (e.g., task delays or resource shortages) can shift a non-critical task onto the critical path. Monitoring can help prevent this.

• Project Flow: Non-critical tasks contribute to the progress. Keeping them on track will ensure smooth project flow and reduce risks.

Monitoring non-critical paths helps avoid risks, keeps resources balanced, and ensures the project runs efficiently.

Critical Path Method Benefits

The following are a few benefits of the Critical Path Method:

It Can Help You Prioritize Resources

You can allocate resources more efficiently by prioritizing critical tasks. This will ensure that the most crucial parts of the project receive the attention and resources that they need to avoid delays. This targeted approach can help prevent project timelines from being extended due to resource shortages.

It Can Help You Track Progress Efficiently

Understanding the critical path allows you to monitor the completion of critical activities more closely. This helps identify early deviations from the planned schedule, allowing timely interventions. Efficient tracking ensures that the project stays on course and that delays can be managed before they impact the overall timeline.

It Visually Shows the Project Timeline and Task Dependencies 

CPM visually represents the project timeline and the dependencies between tasks. You can see tasks’ interconnection and sequence. This visual representation makes understanding the project’s flow easier, identifying potential delays and managing scheduling conflicts. It provides a clear roadmap for project execution and ensures all stakeholders are on the same page.

It Can Help You Find Bottlenecks in Processes

If any task on the critical path is delayed, it can potentially delay the entire project. By analyzing the critical path, you can pinpoint areas where the process may be slowing down or facing constraints. This allows for targeted action to address these bottlenecks, improving overall project efficiency and reducing the risk of extended timelines.

It Can Help You Find Critical Tasks

CPM identifies the critical tasks that can affect the project’s finish date. By focusing on these critical tasks, you can prioritize their completion and ensure they are completed on time. Recognizing these tasks helps allocate appropriate resources, manage risks, and prevent delays.

It is a Good Communication Tool

CPM helps you convey complex project timelines and interdependencies simply. Using visual aids, CPM helps explain the project’s status and progress to stakeholders, team members, and clients. This clarity builds better understanding, collaboration, and coordination throughout the project.

Drawbacks of the Critical Path Method

A few drawbacks of the Critical Path Method are:

It Assumes the Project Has Unlimited Resources

The Critical Path Method is optimistic. It assumes that the project will always have resources whenever they are needed. It also does not consider resource dependencies, which are not always possible. This assumption often leads to delays and additional costs. No organization can provide unlimited resources for all projects; resource constraints are common.

It Can Cause Float Misuse

Misuse of float or slack is routine in the Critical Path Method. According to Parkinson’s Law, “work expands to fill the time available for its completion.” Team members often misuse the slack, thus causing schedule delays. If any activity has float, team members are incentivized to use all of it to complete the task, thus considering float to be a part of the activity duration estimate.

It Can Cause Activity Completion Gain/Loss

If you complete an activity early, the time gained is useless because the next activity must wait until its early start date. This may happen because the resources allocated to the next activity may not be available yet.

However, the opposite is not true. If any activity is delayed, it will delay the next activity, and thus, the project will also be delayed. Delays accumulate in the Critical Path Method, but gain does not.

It Can Cause Student Syndrome

Student Syndrome infects the critical path when team members do not start the task until the last moment. Therefore, when a team member starts the activity at its late start, the activity will have no float, and any delay in the activity will affect the project schedule.

It Has Limited Flexibility

Once the critical path is established, any changes to task durations or dependencies require recalculating the entire project schedule, which can be time consuming. Any change in the network diagram can affect the critical path.

It Can Cause a Lack of Attention Paid to Non-Critical Paths

In the CPM diagram, project managers often pay less attention to non-critical paths, though sometimes they may become critical and make the project manager’s job difficult.

Summary

The Critical Path Method has helped many project managers develop and manage schedules. It is a good communication tool and can help secure stakeholder buy-in. A network diagram has many paths, but you must focus on the critical one. Any delay in critical activity will affect the project schedule. Monitor floats on other paths because if the float drops to zero, then the path will become critical.

With modern advancements in AI, digital tools, and resource optimization, CPM continues to evolve, making project planning more efficient and accurate. By monitoring both critical and non-critical paths, you can minimize risks and ensure successful project delivery.

Further Readings:

• What is the Precedence Diagramming Method?
• What is Critical Chain Project Management?
• What is the PERT Chart?
• What is the Gantt Chart?
• Schedule Compression Techniques
• Fast Tracking Vs Crashing

References:

• Resource Leveling Vs Resource Smoothing
• The ABCs of the Critical Path Method
• Critical Path Analysis

This is an important topic from a PMP exam point of view.